Verification of Universal Quantum Computation

Functionality

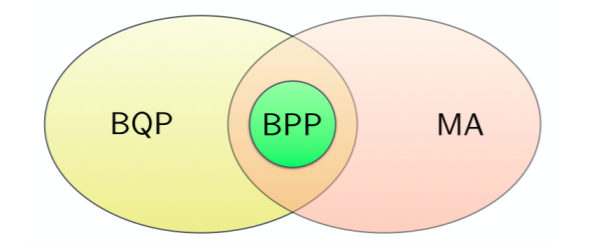
Quantum Computers perform task which are intractable for classical computers. The basic question here would be, "How should one verify the result of a quantum computer? This task is known as quantum verification or verification of quantum computation. BQP is the class of problems that can be solved by a quantum computer and BPP is the class of problems that can be solved by a classical computer. BPP is contained in BQP and hence, there are problems a quantum computer would solve that are intractable for a classical computer, to put it simply. Thus, if in future, an untrusted company claims to have built a quantum computer, how can the consumer be sure of the correctness of the results when he/she (the consumer) cannot compare the results predicted by the proposed quantum computer? This problem is addressed by the functionality, 'verification of quantum computers'. Verification of universal quantum computation targets every computation that can be performed by a quantum computer.

Tags: Quantum Functionality, Universal Task

Protocols

1. Single-prover prepare-and-send: Verifier can only prepare and send quantum states to delegate a BQP computation to the prover
   1. Quantum-authentication based verification:
   2. Trap-based based verification: uses verifiable blind delegated quantum computation
   3. Verification based on repeated runs
2. Single-prover receive-and-measure: Verifier can only receive and measure quantum states
   1. Measurement only verification: uses blind delegated quantum computation
   2. Post-hoc verification: Non-interactive (requires only single round of back and forth communication)
3. Multi-prover entanglement-based: Verifier is completely classical and the provers are entangled
   1. Verification based on CHSH rigidity
   2. Verification based on self-testing graphs
   3. Post-hoc verification

Properties

• Complexity Classes

1. BQP is the class of problems which can be efficiently solved by quantum computers
2. BPP is the class of problems which can be efficiently solved by classical computers.
3. MA (Merlin-Arthur) is the class of problems whose solutions can be verified when given a proof setting called witness.
4. IP (interactive-proof system) is a generalization of MA, which involves back and forth communication between a verifier (a BPP machine) and prover (has unbounded computational power).
5. Protocols 1.1, 1.2 are QPIP protocols and 2.1 is an MIP protocol. QPIP and MIP are classes of decision problems and can be decided by protocols 1.1, 1.2 and 2.1, respectively.

Further Information

• Review Papers

1. Gheorghiu et al (2018): Major portion of this functionality file has been adapted from this review

contributed by Shraddha Singh