Prepare and Measure Quantum Digital Signature
Functionality Description
Digital Signatures (QDS) allow the exchange of classical messages from sender to multiple recipients, with a guarantee that the signature has come from a genuine sender. Additionally, it comes with the properties of (i) transferability i.e. messages with DS can be forwarded from one recipient to another such that DS is verifiable to have come from the original sender, (ii) non-repudiation i.e at any stage after sending the message to one recipient, sender cannot deny having sent the message and corresponding DS, and (iii) unforgeability i.e. a dishonest recipient cannot alter or fake the sender's DS and forward it to other recipients successfully.
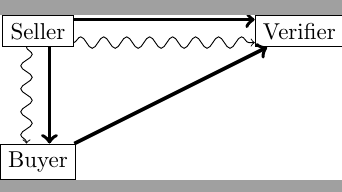
Such protocols require parties to prepare and measure quantum states instantly without having to store them. For simplicity, most protocols take into account the case of one sender and two recipients (Seller, buyer and verifier) exchanging single-bit classical messages.
Tags: Multi Party (three), Quantum Enhanced Classical Functionality, Specific Task, Quantum Digital Signature, Quantum Digital Signature with Quantum Memory, Measurement Device Independent Quantum Digital Signature (MDI-QDS)
Requirements
- Network Stage: Prepare and Measure
- Method: Single quantum state preparation and measurement in two different bases
- Relevant Network Parameters:
- Benchmark values: Length of the keys(L): , Verification threshold per qubit ():, Signing threshold per qubit():, time, scalability, no. of rounds, time, distance, scalability, no. of rounds, threshold values numbers, length of the key
Use Case
Online Transactions, Signing Marksheets
Example:
Outline
Quantum Digital Signature (QDS) protocols can be separated into two stages: the distribution stage, where quantum signals (public keys) are sent to all recipients, and the messaging stage, where classical messages are signed, sent and verified. Here, we take the case of three parties, one sender (referred to as seller) and two receivers (buyer and verifier) sharing a one bit message. Distribution phase can be divided into the following steps:
- Key Distribution: Seller generates her (public key,private key) pair and shares the public key with both receivers in this step. For each possible message (0 or 1), she generates two identical sequences/copies (one for each receiver per possible message) of randomly chosen BB84 ∈ {0,1,+,−} states. The sequence of states is called quantum public key and its classical description, private key. She then sends copies of each quantum public key to the receivers while keeping both the private keys secret to herself. At the end of this step, seller has two private keys, one for each possible message. Similarly, each receiver has two quantum public keys, one for each possible message.
- State Elimination: Receivers store their classical records of the quantum public keys in this step. For each quantum public key received, a receiver randomly chooses X or Z basis for each qubit and measures. Whatever outcome he gets, the receiver is certain that seller could not have generated a state orthogonal to his outcome. So, he records the state orthogonal to his outcome as the eliminated signature element. Such measurement is called ’Quantum State Elimination’. The sequence thus generated by measurement of all the qubits in a public key is called receiver’s eliminated signature for the respective quantum public key. Thus, each receiver finally has two eliminated signatures, one for each possible message.
- Symmetrisation: The two receivers exchange half of their randomly chosen eliminated signature elements. This prevents a dishonest seller succeed in cheating by sending dissimilar public keys to the receivers. Thus ends the distribution phase.
Similarly, Messaging Phase is divided into the following steps:
- Signing: Seller sends desired classical one bit message and the corresponding private key to the desired receiver (called buyer). Buyer compares the private key with his eliminated signature for the corresponding message and counts the number of mismatches (eliminated signature element in seller’s private key).
- Transfer: Buyer forwards the same message and private key to the other receiver (called verifier) who compares it with his eliminated signature for this message.
Properties
- The protocol-
- involves three parties (Seller, Buyer, Verifier) exchanging one-bit classical messages.
- Requires BB84 QKD setup, authenticated quantum and classical channels
- assumes maximum number of participating parties are honest. In the present case at least two parties are honest.
- provides information-theoretic security
- provides security against repudiation, i.e. the probability that seller succeeds in making buyer and seller disagree on the validity of her sent quantum signature decays exponentially with L, as stated by the formula .
- provides security against forgery, i.e. any recipient (verifier) with high probability rejects any message which was not originally sent by the seller herself. Forging probability is given by the formula, , where is 3/8 (calculated using uncertainty principle).
Pseudo Code
- Notations Used:
- L: Length of keys used
- : Threshold value for signing
- : Threshold value for verification
- : Quantum Public key for message k
- : Classical Private key for classical one-bit message k
- : Classical description of qubit in
- : Buyer's Eliminated Signature for message m
- : Verifier's Eliminated Signature for message m
- : Buyer’s random bit to determine the measurement basis of qubit in
- : Verifier’s random bit to determine the measurement basis of qubit in
- : measurement outcome of
Stage 1 Distribution
- Input L
- Output Seller: ; Buyer: ; Verifier:
- Key Distribution:
- For k = 0,1
- Seller prepares quantum public key , where
- She sends Buyer (k,)
- She sends Verifier (k,)
- State Elimination:
- For k = 0,1
- For l = 1,2,...,L
- Buyer chooses
- If , Buyer measures his qubit in X basis
- If , Buyer measures his qubit in Z basis
- return
- For l = 1,2,...,L
- Verifier repeats steps 2(a)-2(b) with randomly chosen basis to get his eliminated signature elements
- Symmetrisation
- For k = 0,1
- Buyer chooses I
- , Buyer sends Verifier
- Verifier chooses J
- , Verifier sends Buyer
- Buyer replaces
- Verifier replaces
- For k = 0,1
Stage 2 Messaging
- Input Seller: Message m, Private Key for m:
- Output Buyer: accept or abort, Verifier: accept or abort
- Signing: ’mismatch’ is when Buyer finds an eliminated signature element in Seller’s private key
- Seller sends Buyer (m,)
- For l = 1,2,..,L
- Buyer counts the number of mismatches () and returns
- If , Buyer accepts m else he aborts
- Transfer
- Buyer sends Verifier (m,)
- For l = 1,2,....,L
- Verifier counts the number of mismatches () and returns
- If , Verifier accepts m else he aborts
Relevant Papers
Theoretical Papers
- WDKA (2015) above example
- DWA (2013)
- first QDS scheme without quantum memory based on Coherent State Comparison.
- Requires Coherent States, authenticated quantum and classical channels, multiports, Unambiguous State Discrimination (USD) (State Elimination), no symmetrisation required.
- Security: Information-theoretic
- AL (2014)
- Establishes coherent state mapping of (2). Replaces SWAP Test with beam splitters. Uses Unambiguous State Discrimination (USD) (State Elimination).
- Requires Phase encoded Coherent states, Balanced Beam Splitters.
- No explicit security proof provided.
- AWA (2015) security proof for generalisation of WDKA (2015) and DWA (2013) to more than two recipients case.
- YFC (2016)
- first QDS scheme without authenticated (trusted) quantum channels. Demonstrates one protocol with two implementation, two copies of single photon method and decoy state method. First uses single qubit photons in three bases; Private key: classical description of states, Public key: pair of non-orthogonal states in any two of the three bases.
- Requires authenticated classical channels, polarisation measurement in three bases, Unambiguous State Discrimination (USD) (State Elimination), uses quantum correlations to check authentication. Decoy State method uses phase-randomised weak coherent states, 50:50 Beam Splitter (BS).
- Security: Information-theoretic.
- AWKA (2015)
- QDS scheme without authenticated quantum channels using parameter estimation phase. Uses a Key Generations Protocol (KGP) where noise threshold for Seller-Buyer and Seller-Verifier is better than when distilling secret key from QKD. Seller sends different key to Buyer and Verifier using KGP. This anamoly is justifiable due to symmetrisation.
- Requires authenticated classical channels, Decoy State QKD setup.
- Security: Information-theoretic.
- WCRZ (2015) demonstrates sending multi-bit classical messages using AWKA (2015) or other similar protocols.
- MH (2016) security proof for generalisation of AWKA (2015) to more than two recipients case.
Experimental Papers


























![{\displaystyle \subset _{R}\{1,2,...,L\},|I|=[L/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/177051edd6cd70195e9f94f8a044005819b28d18)


![{\displaystyle \subset _{R}\{1,2,...,L\},|J|=[L/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9be0d742672958ae27a5466950a74115ba8ab23d)










