Asymmetric Universal 1-2 Cloning: Difference between revisions
| Line 11: | Line 11: | ||
---- | ---- | ||
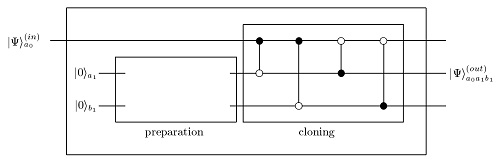
In this protocol, there are three main stages. The first stage is a preparation stage. we prepare two ancillary states with special coefficients which will lead to the desired flow of the information between copied states. The original state will not be engaged at this stage. At the second stage the cloner circuit will act on all the three states (the original and two other states) and at the second stage the two copied state will appear at two of the outputs and one of the outputs should be discarded. The Procedure will be as following: | In this protocol, there are three main stages. The first stage is a preparation stage. we prepare two ancillary states with special coefficients which will lead to the desired flow of the information between copied states. The original state will not be engaged at this stage. At the second stage the cloner circuit will act on all the three states (the original and two other states) and at the second stage the two copied state will appear at two of the outputs and one of the outputs should be discarded. The Procedure will be as following: | ||
[[File:Asymmetriccloner.jpg|right|thumb|1000px| Graphical representation of the network for the asymmetric cloner. The CNOT gates are shown in the cloner section with control qubit (denoted as <math>\bullet</math> ) and a target qubit (denoted as <math>\circ</math> ). We separate the preparation of the quantum copier from the cloning process itself.]] | * Prepare two blank states and then perform a transformation taking these two states to a new state with pre-selected coefficients in such a way that the information distribution between two final states will be the desired.[[File:Asymmetriccloner.jpg|right|thumb|1000px| Graphical representation of the network for the asymmetric cloner. The CNOT gates are shown in the cloner section with control qubit (denoted as <math>\bullet</math> ) and a target qubit (denoted as <math>\circ</math> ). We separate the preparation of the quantum copier from the cloning process itself.]] | ||
*Perform the cloner circuit. the cloner circuit consists of four CNOT gate acting in all the three input qubits. For every CNOT gate, we have a control qubit (which indicates whether or not the CNOT should act) and a target qubit (which is the qubit that CNOT gate acts on it and flips it). | *Perform the cloner circuit. the cloner circuit consists of four CNOT gate acting in all the three input qubits. For every CNOT gate, we have a control qubit (which indicates whether or not the CNOT should act) and a target qubit (which is the qubit that CNOT gate acts on it and flips it). | ||
* The two asymmetric clones will appear at two of the outputs (depending on the preparation stage) and the other output should be discarded. | * The two asymmetric clones will appear at two of the outputs (depending on the preparation stage) and the other output should be discarded. | ||
Revision as of 22:26, 11 November 2018
Functionality Description
Asymmetric universal cloning refers to a quantum cloning machine (QCM) where its output clones are not the same or in other words, they have different fidelities. Here we focus on universal cloning. In asymmetric cloning, we try to distribute information unequally among the copies. A trade-off relation exists between the fidelities, meaning if one of the copies are very close to the original state, the other one will be far from it. There are two approaches to this kind of cloning, both leading to same trade-off relation. Here we discuss the quantum circuit approach (Buzek et al., 1997) It can be also noted that the symmetric universal cloning can be considered as a special case of the asymmetric universal cloning where the information between copies has been equally distributed.
Tags:Building blocks, Quantum Cloning, Universal Cloning, asymmetric cloning, symmetric cloning, copying quantum states, quantum functionality, symmetric or Optimal Cloning, Probabilistic Cloning
Requirements
Example:
Outline
In this protocol, there are three main stages. The first stage is a preparation stage. we prepare two ancillary states with special coefficients which will lead to the desired flow of the information between copied states. The original state will not be engaged at this stage. At the second stage the cloner circuit will act on all the three states (the original and two other states) and at the second stage the two copied state will appear at two of the outputs and one of the outputs should be discarded. The Procedure will be as following:
- Prepare two blank states and then perform a transformation taking these two states to a new state with pre-selected coefficients in such a way that the information distribution between two final states will be the desired.
- Perform the cloner circuit. the cloner circuit consists of four CNOT gate acting in all the three input qubits. For every CNOT gate, we have a control qubit (which indicates whether or not the CNOT should act) and a target qubit (which is the qubit that CNOT gate acts on it and flips it).
- The two asymmetric clones will appear at two of the outputs (depending on the preparation stage) and the other output should be discarded.
Properties
- Notations Used:
- The original input state
- The density matrix of the input pure state equal to
- The scaling parameter of the first clone
- The scaling parameter of the second clone
- The output density matrix of the first clone (equal to if the output state is pure)
- The output density matrix of the second clone (equal to if the output state is pure)
- The ``Identity" or completely mixed density matrix
- state of the ancillary qubits before preparation phase
- state of the ancillary qubits after the preparation
- amplitudes (or coefficients) of the prepared state $|\psi\rangle_{m_1,n_1}$. These coefficients are being used to control the flow of the information between the copies before starting the cloning process.
- The CNOT gate where the control qubit is and the target qubit is
- The total output of the asymmetric cloning circuit
- Bell state
- Plus state. The eigenvector of Pauli X
- The protocol assumes that the original input qubit is unknown and the protocol is independent of the original input state (universality).
- The output copies are not identical and we are able to control the likelihood (fidelity) of the output copies to the original state by pre-preparing the ancillary states with special coefficients.
- Claims for General case:
- Following inequality holds between the scaling factors and
- Following inequality holds between the scaling factors and
- Optimality is provided when the fidelities of two clones, and , saturate the above inequality
- Claims for Special case with bell state:
- Following ellipse equation holds between the scaling factors and
- Following ellipse equation holds between the scaling factors and
- Following equations holds for fidelities of the clones:
Pseudo Code
Input: j qubits where are ancillary and internal states of the QCM.
Stage 1 State preparation
- Prepare N initial states: and blank states:
Stage 2 Unitary transformation
- Perform the following unitary transformation on input state
where
Stage 3: Trace out the QCM state
- Trace out the state of the QCM in states.