Fast Quantum Byzantine Agreement

The classical problem of Byzantine agreement (8) is about reaching agreement in a network of $n$ players out of which $t$ players may be faulty. Each player starts with an input bit $b_{i}$ and the goal is for all correct players to output the same bit $d$ agreement, under the constraint that $d=b_{i}$ at least for some node $i$ validity. The hardness of this task depends on the failure model of the faulty (sometimes called adversary) players. In Byzantine agreement, the faulty players are assumed to show the most severe form of failure known as Byzantine failures. In this model, faulty players behave arbitrarily, can collude and even act maliciously trying to prevent correct players from reaching agreement. Byzantine agreement is an important problem in classical distributed systems, used to guarantee consistency amongst distributed data structures.

Tags: Quantum Enhanced Classical Functionality, Multi Party Protocols, Specific Task, consensus task, failure resistant distributed computing

Assumptions

• We assume that the original input qubit is unknown and the protocol is independent of the original input state (universality).
• The output copies are not identical and we are able to control the likelihood (fidelity) of the output copies to the original state by pre-preparing the ancillary states with special coefficients.

Outline

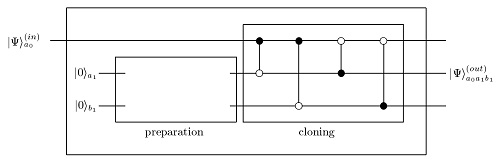
In this protocol, there are three main stages. The first stage is a preparation stage. we prepare two ancillary states with special coefficients which will lead to the desired flow of the information between copied states. The original state will not be engaged at this stage. At the second stage the cloner circuit will act on all the three states (the original and two other states) and at the second stage the two copied state will appear at two of the outputs and one of the outputs should be discarded. The Procedure will be as following:

• Prepare two blank states and then perform a transformation taking these two states to a new state with pre-selected coefficients in such a way that the information distribution between two final states will be the desired.
  

  Graphical representation of the network for the asymmetric cloner. The CNOT gates are shown in the cloner section with control qubit (denoted as $\bullet$ ) and a target qubit (denoted as $\circ$ ). We separate the preparation of the quantum copier from the cloning process itself.
• Perform the cloner circuit. the cloner circuit consists of four CNOT gate acting in all the three input qubits. For every CNOT gate, we have a control qubit (which indicates whether or not the CNOT should act) and a target qubit (which is the qubit that CNOT gate acts on it and flips it).
• The two asymmetric clones will appear at two of the outputs (depending on the preparation stage) and the other output should be discarded.

Notations Used

• • $|\psi \rangle _{in}:$The original input state
  • $\rho _{\psi _{in}}:$ The density matrix of the input pure state equal to $|\psi _{in}\rangle \langle \psi _{in}|$
  • $s_{0}:$ The scaling parameter of the first clone
  • $s_{1}2:$ The scaling parameter of the second clone
  • $\rho _{a}^{out}:$ The output density matrix of the first clone (equal to $|\psi _{a}^{out}\rangle \langle \psi _{a}^{out}|$ if the output state is pure)
  • $\rho _{b}^{out}:$ The output density matrix of the second clone (equal to $|\psi _{b}^{out}\rangle \langle \psi _{b}^{out}|$ if the output state is pure)
  • ${\hat {I}}:$ The ``Identity" or completely mixed density matrix
  • $|0\rangle _{m_{0}}\otimes |0\rangle _{n_{0}}\equiv |00\rangle :$ state of the ancillary qubits before preparation phase
  • $|\psi \rangle _{m_{1},n_{1}}:$ state of the ancillary qubits after the preparation
  • $c_{j}:$ amplitudes (or coefficients) of the prepared state $|\psi\rangle_{m_1,n_1}$. These coefficients are being used to control the flow of the information between the copies before starting the cloning process.
  • $P_{k,l}:$ The CNOT gate where the control qubit is $k$ and the target qubit is $l$
  • $|\psi \rangle _{out}:$ The total output of the asymmetric cloning circuit
  • $|\Phi ^{+}\rangle ={\frac {1}{\sqrt {2}}}(|00\rangle +|11\rangle ):$ Bell state
  • $|+\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle +|1\rangle ):$ Plus state. The eigenvector of Pauli X

Properties

• The protocol assumes that the original input qubit is unknown and the protocol is independent of the original input state (universality).
• The output copies are not identical and we are able to control the likelihood (fidelity) of the output copies to the original state by pre-preparing the ancillary states with special coefficients.
• Claims for General case:
  • Following inequality holds between the scaling factors $s_{0}$ and $s_{1}$
    

$s_{0}^{2}+s_{1}^{2}+s_{0}s_{1}-s_{0}-s_{1}\leq 0$

• • This elliptic inequality shows the possible value of the scaling parameters.
  • Trade-off inequality between the fidelities of the clones:
    

${\sqrt {(1-F_{a})(1-F_{b})}}\geq {\frac {1}{2}}-(1-F_{a})-(1-F_{b})$

• • Optimality is provided when the fidelities of two clones, $F_{a}$ and $F_{b}$, saturate the above inequality
• Claims for Special case with bell state:
  • Following ellipse equation holds between the scaling factors $a$ and $b$
    

$a^{2}+b^{2}+ab=1$

• • Following equations holds for fidelities of the clones:

$F_{a}=1-{\frac {b^{2}}{2}},F_{b}=1-{\frac {a^{2}}{2}}$

Pseudo Code

General Case

For more generality, we use the density matrix representation of the states which includes mixed states as well as pure states. For a simple pure state $|\psi \rangle$ the density matrix representation will be $\rho _{\psi }=|\psi \rangle \langle \psi |$. Let us assume the initial qubit to be in an unknown state $\rho _{\psi }$. Our task is to clone this qubit universally, i.e. input-state independently, in such a way, that we can control the scaling of the original and the clone at the output. In other words, we look for output which can be represented as below:
$\rho _{a}^{out}=s_{0}\rho _{\psi }+{\frac {1-s_{0}}{2}}{\hat {I}}$
$\rho _{b}^{out}=s_{1}\rho _{\psi }+{\frac {1-s_{1}}{2}}{\hat {I}}$
Here we assume that the original qubit after the cloning is “scaled” by the factor $s_{0}$, while the copy is scaled by the factor $s_{1}$. These two scaling parameters are not independent and they are related by a specific inequality.

Stage 1 Cloner State Preparation

1. Prepare the original qubit and two additional blank qubits $m$ and $n$ in pure states: $|0\rangle _{m_{0}}\otimes |0\rangle _{n_{0}}\equiv |00\rangle$
2. Prepare $|\psi \rangle _{m_{1},n_{1}}=c_{1}|00\rangle +c_{2}|01\rangle +c_{3}|10\rangle +c_{4}|11\rangle$, where the complex $c_{i}$ coefficients will be specified so that the flow of information between the clones will be as desired.
   At this stage the original qubit is not involved, but this preparation stage will affect the fidelity of the clones at the end of the process.
3. To prepare the $|\psi \rangle _{m_{1},n_{1}}$ state, a Unitary gate must be performed so that:

$U|00\rangle =|\psi \rangle _{m_{1},n_{1}}$

• Use following relations to specify $c_{j}$ in terms of $a$ and $b$:
  

$c_{1}={\sqrt {\frac {s_{0}+s_{1}}{2}}}$, $c_{2}={\sqrt {\frac {1-s_{0}}{2}}}$, $c_{3}=0$, $c_{4}={\sqrt {\frac {1-s_{1}}{2}}}$
these $c_{j}$ satisfy the scaling equations and also the normalization condition of the state $|\psi \rangle _{m_{1},n_{1}}$. They are being used to control the flow of information between the clones

Stage 2 Cloning Circuit

• The cloning circuit consists of four CNOT gates acting on original and pre-prepared qubits from stage 2. We call the original qubit $|\psi \rangle _{in}$, ``first qubit", the first ancillary qubit of $|\psi \rangle _{m_{1},n_{1}}$, ``second qubit" and the second one, ``third qubit". The CNOT gates will act as follows:

1. First CNOT acts on first and second qubit while the first qubit is control and the second qubit is the target.
2. Second CNOT acts on first and third qubit while the first qubit is control and the third qubit is the target.
3. Third CNOT acts on first and second qubit while the second qubit is control and the first qubit is the target.
4. Forth CNOT acts on first and third qubit while the third qubit is control and the first qubit is the target.

• Mathematically the cloning part of the protocol can be shown as:
  

$|\psi \rangle _{out}=P_{3,1}P_{2,1}P_{1,3}P_{1,2}|\psi \rangle _{in}|\psi \rangle _{m_{1},n_{1}}$

Stage 3 Discarding ancillary state

• Discard one of the extra states. The output states will be the first and second (or third) output.
  
  

Special case with bell state:

Stage 1 Cloner state preparation

1. Prepare the original qubit and two additional blank qubits $m$ and $n$ in pure states: $|0\rangle _{m_{0}}\otimes |0\rangle _{n_{0}}\equiv |00\rangle$
2. Prepare $|\psi \rangle _{m_{1},n_{1}}=a|\Phi ^{+}\rangle _{m_{1},n_{1}}+b|0\rangle _{m_{1}}|+\rangle _{n_{1}}$, where $|\Phi ^{+}\rangle$ is a Bell state and $|+\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle +|1\rangle )$. In this case, the density matrix representation of the output states will be:
   

$\rho _{a}^{out}=(1-b^{2})|\psi \rangle \langle \psi |+{\frac {b^{2}}{2}}{\hat {I}}$
$\rho _{b}^{out}=(1-a^{2})|\psi \rangle \langle \psi |+{\frac {a^{2}}{2}}{\hat {I}}$
Stage 2 Cloning Circuit

• The cloning circuit is exactly the same as the general case. after the cloning circuit, the output state will be:
  

$a|\psi \rangle _{in}|\Phi ^{+}\rangle _{m,n}+b|\psi \rangle _{m}|\Phi ^{+}\rangle _{in,n}$ The reduced density matrix of two clones A and B can be written in terms of their fidelities:
$\rho _{a}^{out}=F_{a}|\psi \rangle \langle \psi |+(1-F_{a})|\psi ^{\perp }\rangle \langle \psi ^{\perp }|$
$\rho _{b}^{out}=F_{b}|\psi \rangle \langle \psi |+(1-F_{b})|\psi ^{\perp }\rangle \langle \psi ^{\perp }|$
Stage 3 Discarding ancillary state

• The same as the general case.

Further Information

• The protocol (3) is based on the classical protocol of (7), where the classical Oblivious Common Coin is replaced by a Quantum version, which is based on the Verifiable Quantum Secret Sharing Scheme presented in (4). The protocol of (7) also runs in constant expected time, but can only deal with limited-information adversaries. This means that the adversaries can not read communication between honest parties and read their internal state. The classical lower bound in the same model of $\Omega ({\sqrt {n\log n}})$ is proven in (6).
• The work (3) also provides a protocol in a weaker failure model known as fail-stop failures. Here the nodes will crash and stop working indefinitely (stop responding). Another protocol in the same model is presented in (2).
• Another weakened version of the problem, known as detectable byzantine agreement, is solved with quantum resources in (5) (and following works). In detectable byzantine agreement, the protocol is also allowed to abort (upon detecting failures) instead of reaching agreement.

References

1. TNM (2017)
2. LS (2010)
3. BH (2005)
4. CGS (2002)
5. FGM (2001)
6. JB (1998)
7. FM (1997)
8. LSP (1982)

Further Information

*contributed by Bas Dirke