Supplementary Information: Difference between revisions
mNo edit summary |
|||
| Line 5: | Line 5: | ||
<math>\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1}),</math></br> | <math>\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1}),</math></br> | ||
<math>\ket{-}=\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})</math> | <math>\ket{-}=\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})</math> | ||
</br>X (NOT gate): <math>X\ket{0}\,\to\,\ \ket{1}, X\ket{1}\,\to\,\ \ket{0}, X\ket{+}\,\to\,\ \ket{+}, X\ket{-}\,\to\,\ -\ket{-}</math> | |||
</br>X (NOT gate): <math>X\ket{0}\,\to\,\ \ket{1}, | </br>Z (Phase gate): <math>Z\ket{+}\,\to\,\ \ket{-}, Z\ket{-}\,\to\,\ \ket{+}, Z\ket{0}\,\to\,\ \ket{0}, Z\ket{1}\,\to\,\ -\ket{1}</math></br> | ||
</br>Z (Phase gate): <math>Z\ket{+}\,\to\,\ \ket{-}, | |||
Thus, <math>\ket{0}</math>, <math>\ket{1}</math> are eigenstates of Z gate and <math>\ket{+}</math>, <math>\ket{-}</math> are eigenstates of X gate. | Thus, <math>\ket{0}</math>, <math>\ket{1}</math> are eigenstates of Z gate and <math>\ket{+}</math>, <math>\ket{-}</math> are eigenstates of X gate. | ||
</br> (Hadamard gate): <math>H\ket{0}\,\to\,\ \ket{+}</math> or <math>H\ket{1}\,\to\,\ \ket{-}</math> | </br> (Hadamard gate): <math>H\ket{0}\,\to\,\ \ket{+}</math> or <math>H\ket{1}\,\to\,\ \ket{-}</math> | ||
Revision as of 14:38, 7 December 2018
A General Introduction to Quantum Information
Quantum computation is marked by a set of unitary matrices (quantum gates) acting on qubit states followed by measurement. The most used representation is the circuit model of computation, comprising straight lines and boxes. The horizontal lines represent qubits and boxes represent single qubit unitary gates. A two qubit unitary gate links one qubit from another via vertical lines. Some useful notations are given below.
Failed to parse (unknown function "\ket"): {\displaystyle \ket{+}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1}),}
Failed to parse (unknown function "\ket"): {\displaystyle \ket{-}=\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})}
X (NOT gate): Failed to parse (unknown function "\ket"): {\displaystyle X\ket{0}\,\to\,\ \ket{1}, X\ket{1}\,\to\,\ \ket{0}, X\ket{+}\,\to\,\ \ket{+}, X\ket{-}\,\to\,\ -\ket{-}}
Z (Phase gate): Failed to parse (unknown function "\ket"): {\displaystyle Z\ket{+}\,\to\,\ \ket{-}, Z\ket{-}\,\to\,\ \ket{+}, Z\ket{0}\,\to\,\ \ket{0}, Z\ket{1}\,\to\,\ -\ket{1}}
Thus, Failed to parse (unknown function "\ket"): {\displaystyle \ket{0}}
, Failed to parse (unknown function "\ket"): {\displaystyle \ket{1}}
are eigenstates of Z gate and Failed to parse (unknown function "\ket"): {\displaystyle \ket{+}}
, Failed to parse (unknown function "\ket"): {\displaystyle \ket{-}}
are eigenstates of X gate.
(Hadamard gate): Failed to parse (unknown function "\ket"): {\displaystyle H\ket{0}\,\to\,\ \ket{+}}
or Failed to parse (unknown function "\ket"): {\displaystyle H\ket{1}\,\to\,\ \ket{-}}
Unitary Operation
Hierarchy of Quantum Gates
There are different class of quantum gates as follows,
- Pauli Gates(U): Single Qubit Gates I (Identity), X, Y, Z. All the gates in this set follow U2 = I
- Clifford Gates(C): Pauli Gates, Phase Gate, C-NOT. This set of gates can be simulated on classical computer. All the gates in this set follow CU=U’C, where U and U’ are two different Pauli gates depending on C
- Toffoli Gate: A three qubit gate that does not belong to Clifford Group
- T Gates: \sqrt{Z} Although a member of Clifford Gate, its eigen states can be used as acillas to make quantum gate sthat are not!
- Universal Set of gates: This set consists of all Clifford gates and one Non-Clifford gate (or T gate). One can also say one Toffoli gate and Hadamard gate constitute the set of Universal Gates. If a model can realise Universal Set of gates, it can imlpement any quantum computation efficiently. T gates follow UT = PaU0T, where P is the phase gate and U, U’ are any two Pauli gates depending on C. Parameter 1 is obtained from U, such that P0 = I, P1 = P.
To summarize, the hierarchy of quantum can be defined as such.
If C(1)=P, C(2)=C, C(3)=T, then
C(n)={U:UQU\dagger=C(n-1),Q\epsilon C(1)}
Magic States
Eigen states of T gates
Universal Resource
A set of \ket{+_\theta} states on which applying Clifford operations is enough for universal quantum computation.
Classical Quantum State
Density Matrices
Fidelity
Quantum Information Primitives
Superposition
Entanglement
Measurement
Discrete Variables and Continuous Variables
Complexity
- BQP
- MA
- BPP
Security Definitions
- Quantum Honest But Curious
- Malicious
- Chosen Plain-text Attack (CPA)
- Learning With Errors
Quantum Cryptography Techniques
Quantum One Time Pad
- Pauli Gates
- Clifford Gates
- T Gates
Gate Teleportation
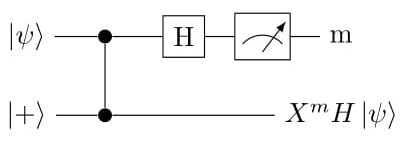
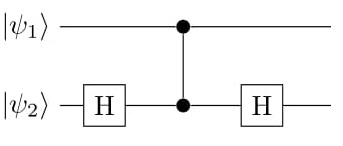
The idea comes from one-qubit teleporation. This means that one can transfer an unknown qubit |ψi without actually sending it via a quantum channel. The underlying equations explain the notion. See Figure 1 for circuit.
(H ⊗ I)(CZ12)|ψi1 |+i2
= (H ⊗ I)(CZ12)(a|0i1 + b|1i1)|+i2
= (H ⊗ I)(a|0i1 |+i2 + b|1i1 |−i2)
= a|+i1 |+i2 + b|−i1 |−i2
= |0i1 ⊗ (a|+i2 + b|−i2) + |1i1 ⊗ (a|+i2 − b|−i2)
= |0i1 ⊗ (a|+i2 + b|−i2) + |1i1 ⊗ X(a|+i2 + b|−i2)
= |0i1 ⊗ H(a|0i2 + b|1i2) + |1i1 ⊗ XH(a|0i2 + b|1i2)
= |0i1 ⊗ H |ψi2 + |1i1 ⊗ X |ψi2
= |mi ⊗ XmH |ψi
Similarly if we have the input state rotated by a Z(θ) gate the circuit would look like Figure 2a. As the rotation gate Z(θ) commutes with Controlled-Phase gate. Hence, Figure 2b is justified.
This shows that for a pair of C-Z entangled qubits, if the second qubit is in |+i state (not an eigen value of Z) then one can teleport (transfer) the first qubit state operated by any unitary gate U to the second qubit by performing operations only on the first qubit and measuring it. Next, we would need to make certain Pauli corrections (in this case Xm) to obtain U |ψi. In other words, we can say the operated state is teleported to the second qubit by a rotated basis measurement of the first qubit with additional Pauli corrections.
Graph states
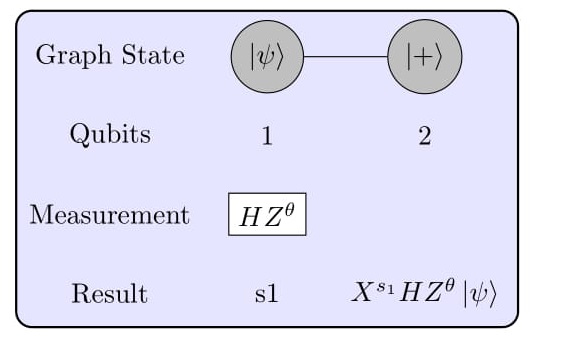
The above operation can also be viewed as a graph state with two nodes and one edge. The qubit 1 is measured in a rotated basis HZ(θ), thus leaving qubit 2 in desired state and Pauli Correction Xs1HZ(θ1)|ψi, where s1 is the measurement outcome of qubit 1.Figure 3
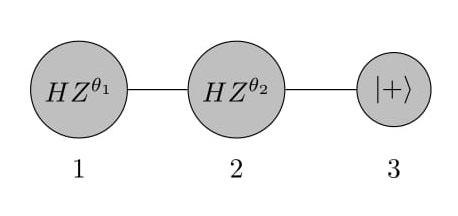
Now, suppose we need to operate the state with two unitary gates Z(θ1) and Z(θ2). This can be done by taking the output state of Z(θ1) gate as the input state of Z(θ2) gate and then repeating gate teleportation for this setup, as described above. Thus, following the same pattern for graph states we have now three nodes (two measurement qubits for two operators and one output qubit) with two edges, entangled as one dimensional chain(See Figure 4).
The measurement on qubit 1 will operate Xs1HZ(θ1)|ψi⊗I on qubits 2 and 3. If qubit 2 when measured in the given basis yields outcome s2, qubit 3 results in the following state Xs2HZ(θ2)Xs1HZ(θ1)|ψi. Using the relation we shift all the Pauli corrections to one end i.e. qubit 3 becomes Xs2Zs1HZ(±θ2)HZ(θ1)|ψi{equation missing}(Zs1H = HXs1). This method of computation requires sequential measurement of states i.e. all the states should not be measured simultaneously. As outcome of qubit 1 can be used to choose sign of ±θ2. This technique is also known as adaptive measurement. With each measurement, the qubits before the one measured at present have been destroyed by measurement. It is a feed-forward mechanism, hence known as one way quantum computation.
Measurement Based Quantum Computation (MBQC)
MBQC is a formalism used for quantum computation by operating only single qubit measurements on a fixed set of entangled states, also known as graph states. Graph states denote any graph where each node represents a quantum state, and the edges denote entanglement between any two vertices. The measurement on successive layers of qubits is decided by previous measurement outcomes. Outcomes of last qubit layer gives the result of concerned computation. Following, we illustrate certain primitives necessary to understand the working of MBQC.
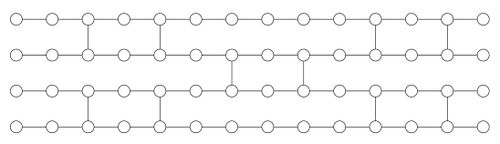
Cluster States
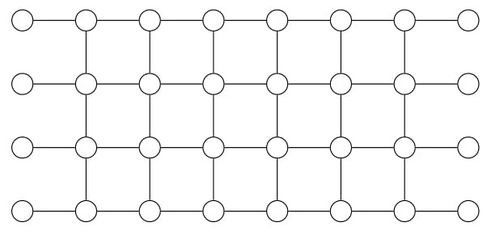
In case of multi-qubit quatum circuits, one needs a 2-dimensional graph state. Cluster State is a square lattice used as substrate for such computation. All the nodes are in |+i entangled by C-Z indicated by the edges. It is known to be universal i.e. it can simulate any quatum gate.
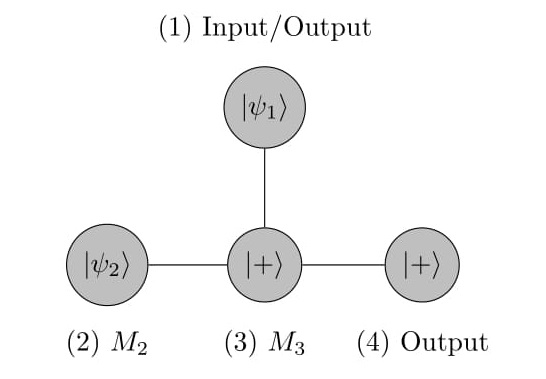
Each row would thus represent the teleporation of starting qubit in that row horizontally. On the other hand, vertical edges indicate different input qubits linked with multi-qubit gates (same as circuit model). For example, see Figure Figure 6 to understand the conversion from circuit model to graph state model. As the computation relation follows X = HZH, thus, Figure Figure 6a represents Circuit diagram for C-NOT gate in terms of C-Z gate and Single Qubit Gate H.
Figure 6b shows implementation of the first Hadamard gate on the second input state as measurement M2 on qubit 2. Then C-Z gate is implemented by the entangled qubits 3 and 1 in the graph state. Qubit 3 is entangled to another qubit 4 to record the output while measurement M3 on qubit 3 implements the second Hadamard gate. Finally, the states to which qubits (1) and (4) are reduced to determine the output states of the two input qubits after C-NOT gate operation. It is evident that one needs to remove certain nodes from the cluster state in order to implement the above shown graph state. This can be done by Z-basis measurements. Such measurements would leave the remaining qubits in the cluster state with extra Pauli corrections. This can be explained as follows. Consider a 2-dimesional graph state {1,2}. If qubit 1 is to be eliminated, we operate C-Z with 2 as target and 1 as control.
CZ12 |+i1 |+i2 = |0i1 |+i2 + |1i1 |−i2 ,
Thus, if measurement on 1 yields m, qubit 2 would be in the state Zm |+i. Hence, such Z-basis measurements invoke an extra Zm Pauli correction on all the neigbouring sites of 1 with 1 eliminated, in the resulting graph state. Thus, to summarise, we design a measurement pattern from gate teleportation circuit of the desired computation as shown above. The cluster state is converted into the required graph state by Z-basis measurement on extraneous sites. Measuring all the qubits in the required basis and we get the required computation in the form of classical outcome register from measurement of the last layer of qubits. If it is a quantum function, the last layer of qubits is the output quantum register.
Brickwork States
Although cluster states are universal for MBQC, yet we need to tailor these to the specific computation by performing some computational (Z) basis measurements. If we were to use this principle for blind quantum computing, Client would have to reveal information about the structure of the underlying graph state. Thus, for the UBQC protocol, we introduce a new family of states called the Brickwork states which are universal for X − Y plane measurements and thus do not require the initial computational basis measurements. It was later shown that the Z-basis measurements can be dropped for cluster states and hence cluster states are also universal in X-Y measurements.
Definition 1 A brickwork state Gn×m, where m ≡ 5 (mod 8), is an entangled state of n × m qubits constructed as follows (see also Figure 7):
- Prepare all qubits in state |+i and assign to each qubit an index (i,j), i being a column (i ∈ [n]) and j being a row (j ∈ [m]).
- For each row, apply the operator c-Z on qubits (i,j) and (i,j + 1) where 1 ≤ j ≤ m − 1.
- For each column j ≡ 3 (mod 8) and each odd row i, apply the operator c-Z on qubits (i,j) and (i + 1,j) and also on qubits (i,j + 2) and (i + 1,j + 2).
- For each column j ≡ 7 (mod 8) and each even row i, apply the operator c-Z on qubits (i,j) and (i + 1,j) and also on qubits (i,j + 2) and (i + 1,j + 2).
Flow Construction-Determinism
Measurement outcomes of qubits is not certain, hence it renders MBQC a non-deterministic model. This can still be rectified by invoking Pauli corrections based on the previous outcomes, as evident from above. For example, to implement Hadamard gate on input state |ψi = a|0i + b|1i, we consider the case of a two qubit graph state C2x1.
C2x1 = CZij |ψii |+ij = a|00i + a|01i + b|10i − b|11i
If one measures qubit i in {|+i,|−i} basis and gets outcome s, qubit j reduces to,
= (a + b)|0i + (a − b)|1i,if s=0
= (a − b)|0i + (a + b)|1i,if s=1
As, the two possible output states are different, it shows this method is non-deterministic. One could end up with any of the two states and there is no certainty. Nevertheless, we observe that if X gate is operated on the second qubit after measurement if outcome is 1, both the equations would be same and hence, obtained state is H |ψi.
Flow construction is the semanticism to construct the measurement pattern for a given graph state. It gives the Pauli corrections for a particular qubit in the graph state, called X and Z dependencies. In simpler words, it records the effect of shifting all Pauli X and Z corrections to the left of (after performing) Entanglement and Entanglement operations, respectively, for each qubit. The result is recorded as sets of X, Z corrections required for each site. These sets depend on the graph state and not the computation or measurement results. Hence, it can be computed while choosing the graph state for a required computation. Following we illustrate how to construct such models with ease using Measurement Calculus to invoke determinism in One-Way Quantum Computation(MBQC).
Choose a unitary gate for the circuit and hence, its measurement pattern. In order to implement this pattern on a graph state, there are four basic steps: Preparation, Entanglement, Measurement, Corrections.
- Preparation prepares all input qubits in the required state, generally represented as |+θi = ) where
- Entanglement entangles all the qubits according to the required graph state. This operation is denoted by Eij, where C-Z is operated with i as control qubit and j as target qubit.
- Measurement assigns measurement angle in X-Y plane for each qubit. Measurement operator is notated as Miα: the qubit ’i’ would be measured in {|+αi,|−αi} basis i.e. if the state is ) one gets outcome 0 and if the state is ), the outcome is 1.
- Correction calculates all Pauli corrections to be applied on a given qubit in the pattern. The set of such parameters are called Dependencies for X and Z operators individually. To calculate all the Pauli Corrections on a given qubit, one needs to take into account the measurement outcomes of previous qubits as well as commutation relations. Both affect the Pauli corrections for a given qubit. Below is a formalism to explain the process with an example.
The effect of X gate on a measurement angle (α) in X-Y plane is to change its sign and Z gate is to add a phase π.
t α s α t s (−1)sα+tπ [Mi ] = Mi Z X = Mi{equation missing}π
We shall denote measurement in X-basis ({equation missing} and Y-basis ({equation missing}
Commutation relations:
EijXis = XisZisEij (EX)
EijXjs = XjsZjsEij (EX)
EijZit = ZitEij (EZ){equation missing}
= (EZ){equation missing}
t α s r
[Mi ] Xi = t α s+r[Mi ]{equation missing}(MX)
MixXis = Mix (MX){equation missing}
= (MZ){equation missing}
The last second equation is implied from the fact that for , x=0=-0. Thus, X gate has no effect on measurement in X-basis for the given states. Using above notations we express the equation for circuit model of C-NOT from Figure 6 with two inputs and two outputs: Qubits: 1,2,3,4
Outcomes: s1,s2,s3,s4
Circuit Operation: .
EX =⇒{equation missing}
EX =⇒{equation missing}
MX =⇒{equation missing}
X4s3Z4s2Z1s2M3xM2xE13E234{equation missing}
Hence, we obtain a measurement pattern to implement C-NOT gate with a T-shaped graph state with three qubits entangled chain {2,3,4} and 1 entangled to 3. X dependency sets for qubit 1:{s3}, 2:φ, 3:φ, 4:φ. Z dependency sets for qubit 1:{s2}, 2:φ, 3:φ, 4:{s2}. The measurements are independent of any outcome so they can all be performed in parallel. In the end, Pauli corrections are performed as such. Parity (modulo 2 sum) of all the previous outcomes in the dependency set is calculated for each qubit{equation missing} (i), for X (sXi = s1 ⊕ s2 ⊕ ...) and Z (sZi = s1 ⊕ s2 ⊕ ...), separately. Thus, is operated on qubit i.{equation missing}
Quantum Capable Homomorphic Encryption
- Homomorphic Encryption
A homomorphic encryption scheme HE is a scheme to carry out classical computation from the Server while hiding the inputs, outputs and computation. It can be divided into following four stages. - Key Generation. The algorithm (pk,evk,sk) ← HE.Keygen(1λ) takes a λ, a security parameter as input and outputs a public key encryption key pk, a public evaluation key evk and a secret decryption key sk.
- Encryption. The algorithm c ← HE.Encpk(µ) takes the public key pk and a single bit message µ ∈ {0,1} and outputs a ciphertext c. The notation HE.Encpk(µ;r) is be used to represent the encryption of a bit µ using randomness r.
- Decryption. The algorithm µ∗ ← HE.Decsk(c) takes the secret key sk and a ciphertext c and outputs a message µ∗ ∈ {0,1}.
- Homomorphic Evaluation The algorithm cf ← HE.Evalevk(f,c1,...,cl) takes the evaluation key evk, a function f : {0,1}l → {0,1} and a set of l ciphertexts c1,...,cl, and outputs a ciphertext cf. It must be the case that:
HE.Decsk(cf) = f(HE.Decsk(c1),...,HE.Decsk(cl)) (1) with all but negligible probability in λ. This means classical HE decrypts ciphertext bit by bit. HE scheme is compact if HE.Eval is independent of any inputs or computation. It is fully homomorphic if it can compute any boolean computation.
- Quantum Capable
A classical HE is quantum capable if it can be used to evaluate quantum circuits.
Any HE scheme to be quantum capable requires the following two properties.
- invariance of ciphertext:
- natural XOR operation:
Garden Hose Complexity Model
- Gadget Construction for QFHE
Trapdoor Claw-Free Function (TCF)
Fault Tolerance
Quantum Error Correction
- Quantum Error Correcting Codes (QECCs)
- Stabilizer Codes